Applying Benfords Law

If you don’t know about Benford’s law here is a quick summary:

In numerical data the frequency distribution of the leading digits it not an equal distribution. The lower the digit the more likely it is to appear as leading digit in the data. For example in base 10: Numbers with the initial digit 1 occur about 6.6 times as often as numbers with the initial digit 9.

For more information check out the extensive Wikipedia page about Benford’s law.

NFL Salary Data

Salary data from 1765 NFL players. Numbers starting with digit 1 to 9: 310, 109, 114, 361, 276, 315, 132, 67, 81.

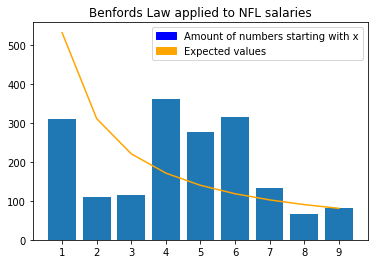
Since most of the players earn less then a million dollar the distribution of salary numbers is not enough dispersed for the salary numbers to follow Benford’s law. Because many players earn between $400,000 and $600,000 the digits 5, 6, 7 are over represented while digits 1, 2, 3 are under represented.

Wikipedia Pages about Benford’s law

The pages used for the analysis were the englisch Wikipedia page about Benford’s law and all the translations of it found in the sidebar. There are 1846 numbers in all the Wikipedia pages about Benford’s law.

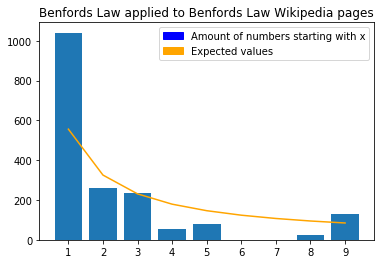
As you can see the actual amount of numbers found on all the Wikipedia pages about Benford’s law don’t match up with what you would expect from Benford’s law. The amount of ones is nearly double of what you would expect and there are no numbers starting with six or seven in any of the pages.

The amount of numbers starting with digit 1 to 9 are: 1040, 260, 234, 52, 78, 0, 0, 26, 130.

It seems to me that Benford’s law didn’t work for this dataset is that the numbers aren’t from a genuinely random source.

Boiling and melting points of Elements

Finally a working example. The boiling and melting points of elements from the periodic table. With 203 data points the sample size if quite small but it still results in the best results so far. The digits appear this many times from 1 to 9: 68, 38, 39, 17, 13, 9, 4, 4, 10.

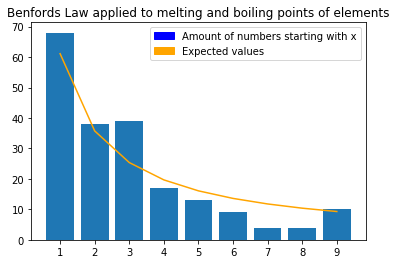
The way I see it the data points are dispersed enough, elements can have melting and boiling points between -34°C and 1100°C, and thats why Benford’s law applies to this dataset.